[Ir a Inicio] [Ir a Contenidos]

Vimos que cuando f(x) es la razón de cambio de la función F(x) y f(x) ³ 0 en [a, b] entonces la integral definida tiene la siguiente interpretación:

= cambio total en F(x) cuando x cambia de a a b.

Decir que f(x) es la razón de cambio de F(x) significa que f(x) es la derivada de F(x) o  equivalentemente que F(x) es una primitiva de f(x). El cambio total en F(x) cuando x cambia de a a b es la diferencia entre el valor de F al final y el valor de F al principio, es decir, F(b) - F(a). Podemos definir = F(b) - F(a).

Esta definición o principio se puede aplicar a todas las razones de cambio en las ciencias sociales y naturales. A modo de ejemplo podemos citar:

Si v(t) es el volumen de agua de un depósito, en el instante t, entonces su derivada v'(t) es la razón a la cual fluye el agua hacia el depósito en el instante t. Así = v(t₂) - v(t₁) es el cambio en la cantidad de agua en el depósito entre los instantes t₁ y t₂.

Si [c](t) es la concentración del producto de una reacción química en el instante t entonces la velocidad de reacción es la derivada [c]'(t). De esta manera = [c](t₂) - [c](t₁) es el cambio en la concentración [c] desde el instante t₁ hasta el t₂.

Si la masa de una varilla, medida desde la izquierda hasta un punto x, es m(x) entonces la densidad lineal es r (x) = m'(x). De esta manera = m(b) - m(a) es la masa del segmento de la varilla entre x = a y x = b.

Si la tasa de crecimiento de una población es entonces = p(t₂) - p(t₁) es el aumento de población durante el período desde t₁ hasta t₂.

Si c(x) es el costo para producir x unidades de un artículo, entonces el costo marginal es la derivada c'(t). Por consiguiente = c(x₂) - c(x₁) es el incremento en el costo cuando la producción aumenta desde x₁ hasta x₂ unidades.

Si un objeto se mueve a lo largo de una recta con función de posición s(t) , entonces su velocidad es v(t) = s'(t) de modo que = s(t₂) - s(t₁) es el cambio de la posición, o desplazamiento, de la partícula durante el período desde t₁ hasta t₂.

Dado que la aceleración de un objeto es a(t) = v'(t), podemos asegurar que la expresión

= v(t₂) - v(t₁) es el cambio en la velocidad en el instante t₁ hasta el t₂.

La potencia P(t) indica la razón de cambio de la energía E(t). Esto permite decir que P(t) = E'(t) y por lo tanto resulta = E(t₂) - E(t₁) indica la energía utilizada en el tiempo entre t₁ y t₂.

La definición que estudiamos de integral definida nos permite calcular o evaluar la integral de funciones sencillas pero en la mayoría de los casos el cálculo del límite de sumas resulta complicado.

LA INTEGRAL DEFINIDA COMO FUNCIÓN

 Ahora sí podemos avanzar ....

Sea f una función continua en un intervalo [a, b]. Definimos una nueva función g dada por g(x) = donde a £ x £ b. Se observa que g sólo depende de x, variable que aparece como límite superior en el cálculo de la integral.

Si x es un número fijo, entonces la integral es un número definido. Si hacemos que x varíe, el número también varía y define una función que depende de x.

Analicemos una función continua f(x) siendo f(x) ³ 0.

Podemos decir que g(x) = se puede interpretar como el área debajo de la gráfica de f desde a hasta x, donde x puede variar desde a hasta b (se debe pensar en g como la función "el área hasta").

El TEOREMA FUNDAMENTAL DEL CÁLCULO

Primera Parte

Si f es una función continua en [a, b] entonces la función donde a £ x £ b es derivable y verifica A' (x) = f(x) para todo x del intervalo.

Ahora estamos en mejores condiciones para comprender la demostración del teorema.

Demostración: Queremos calcular

Pero según la definición de A(x) resulta:

De aquí el numerador: (1)

Por propiedades de la integral definida

Reemplazando en (1), surge

Es decir y por lo tanto:

Si observamos el siguiente gráfico, vemos que:

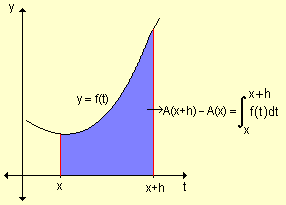
De aquí surge que si m es el mínimo valor y M es el máximo que toma la función en el intervalo [x, x+h], el área de la región sombreada estará comprendida entre el área del rectángulo de base h y altura m, y el área del rectángulo de base h y altura M.

Suponemos h > 0 (se demuestra de manera análoga para h < 0).

Dividiendo por h, resulta: .

Pero cuando h ® 0, el intervalo [x, x+h] tiende a reducirse a un único punto x y por lo tanto los valores m y M tienden a f(x).

Por lo tanto:

Luego

Segunda Parte

Si f es una función continua en el intervalo [a, b] y F una primitiva cualquiera, entonces:

Demostración:

Según la primera parte del teorema

Si F(x) es otra primitiva, se tiene que A(x) = F(x) + k

Si x toma el valor a, se verifica que A(a) = F(a) + k pero como entonces F(a) = -k  y A(x) = F(x) - F(a).

Si además sustituimos x por b, resulta A(b) = F(b) - F(a) , es decir:

Si F es cualquier primitiva .

A esta forma práctica de trabajo se la conoce como REGLA DE BARROW.

.

Ejemplo: Determine el valor de

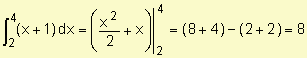
Tomadas juntas las dos partes del teorema fundamental expresan que la derivación y la integración son procesos inversos. Se puede decir, en un lenguaje coloquial que cada una "deshace lo que hace la otra".

Observación: el teorema fundamental del cálculo no requiere que la función sea positiva. Sirve para evaluar las integrales definidas y muestra la estrecha relación existente entre la derivada y la integral.

La integral definida como función y la regla de Barrow a través de un ejemplo.

Halle la función F(x) = en x = 0, , 1, y 2.

Podemos hallar el valor de cada una de las cinco integrales definidas cambiando por los límites superiores pedido, pero es mucho más sencillo fijar x (como una constante temporalmente) y aplicar el teorema fundamental del cálculo con lo que obtenemos.

Resulta la función F(x) = = = 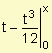que se debe evaluar en los distintos valores de x solicitados.

Si derivamos se obtiene F'(x) == f(x) que coincide con el integrando.

Ejemplo: Encuentre el valor de a si se sabe que

Integrando y aplicando la regla de Barrow obtenemos:

= =

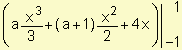Igualando y despejando a resulta: = Þ = Þ a = 2

Ejemplo: Halle si f(x) = .

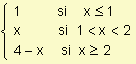La función f(x) es por tramos, en consecuencia:

= =

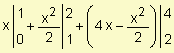
= (1- 0) + = .

Para ampliar los conocimientos de la relación entre la integral definida y el cálculo de primitivas puede consultar la página http://www.cnice.mecd.es/Descartes/Bach_CNST_2/La_integral_definida_y_la_funcion_area/fintegral.html

[Ir a Inicio] [Ir a Contenidos]