donde n
indica la cantidad de subdivisiones del intervalo, es decir la cantidad de
rectángulos que formamos si hacemos el mismo razonamiento que en la
situación
4.[Volver a El problema de la distancia] [Ir a Inicio]
| Situación 5. El cálculo de efectos de cambio con razones de cambio variables. Se conoce la relación funcional que vincula la velocidad con el tiempo. |
Un joven entrena para su competencia en los próximos juegos deportivos de la ciudad en una bicicleta fija durante una hora cada día de modo que en cualquier tiempo t, medido en horas, su velocidad es v(t) = 36t2 + 3 kilómetros por hora. Si queremos hallar la distancia ficticia recorrida por el ciclista durante su hora de entrenamiento podemos subdividir la hora en minutos, segundos, fracciones de segundo e ir calculando la distancia recorrida en cada período. La suma de las distancias en cada intervalo de tiempo nos dará la distancia total que recorrería durante la hora completa. Dado que el momento inicial se considera en t = 0 trabajamos en el intervalo [0, 1].
Podemos pensar que, la longitud de
cada subintervalo es D t =
donde n
indica la cantidad de subdivisiones del intervalo, es decir la cantidad de
rectángulos que formamos si hacemos el mismo razonamiento que en la
situación
4.
Surge ahora la posibilidad de utilizar el valor de la función en el extremo izquierdo, en el extremo derecho ó, por ejemplo, en el punto medio de cada intervalo. El subíndice i indica cada uno de los n subintervalos considerados.
1. Extremo izquierdo de cada
subintervalo = ti
= 
2. Extremo derecho de cada subintervalo
= ti
= 
3 . Punto medio de cada subintervalo
= ti
= 
= 
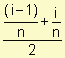Calculamos la distancia recorrida en cada subintervalo
1. Utilizando el valor de la función en el extremo izquierdo del intervalo:
di
= v(ti)
. D t =
=
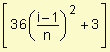
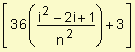
di
= 
=
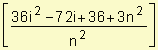
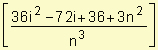
2. Utilizando el valor de la función en el extremo derecho del intervalo:
di
= v(ti)
. D t =
=
=
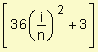
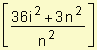
di
= 
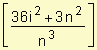
3. Utilizando el valor de la función en el punto medio del intervalo:
di
= v(ti)
. D t =
=
=
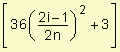
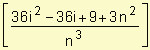
Para obtener el valor de la distancia total debemos sumar las distancias recorridas en cada intervalo. Planteamos en cada caso la sumatoria correspondiente:
1. Distancia total =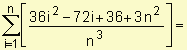
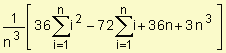
En el desarrollo tenemos en cuenta que
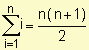y
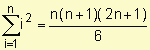
Distancia total =
Distancia total =
]
Distancia total =
Distancia total =
2. Distancia total =
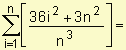
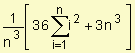
Distancia total =
=
Distancia total =
3. Distancia total =
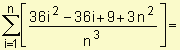
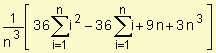
Distancia total =
Distancia total =
Distancia total =
Si en los tres casos consideramos el
valor que D t =
tiende a
cero, es decir que consideramos una cantidad lo suficientemente grande de
rectángulos, n tiende a infinito podemos asegurar que en los tres
casos la distancia total recorrida es de 15 km. dado que:
1. 
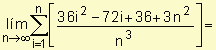
= 15
2.
= 15
3. 
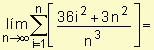
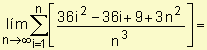
= 15
Si realizamos la gráfica de la velocidad con respecto al tiempo en el intervalo [0, 1] en cada uno de los casos planteados, ¿qué podemos decir con respecto a la distancia y el área de los rectángulos de medida de la base igual a D t y altura coincidente con el valor de la velocidad definida en algún punto del subintervalo cuando la cantidad de rectángulos tiende a infinito? |
Para tener en cuenta: para hallar la distancia recorrida por un móvil si se conoce la velocidad del mismo en todos los momentos necesitamos resolver un tipo especial de límite. |
[Volver a El problema de la distancia] [Ir a Inicio]