[Volver a Límite de funciones] [Ir a Contenidos] [Ir a Inicio]
Un límite importante
Se puede demostrar que
Al evaluar el numerador y el
denominador en x = 0, se obtiene la
indeterminación 
.
Para resolverlo, no pueden utilizarse las técnicas vistas
anteriormente, pero sin embargo, el 
existe y vale 1.
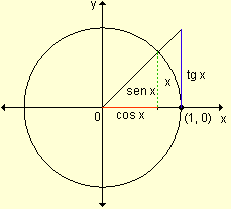
Sea un ángulo cuya medida en
radianes sea x, 0 < x < 
.
| Observando la gráfica
resulta:
sen x < x < tg x Como sen x ¹ 0, dividiendo por sen x se obtiene:
Dado que resulta: 1 < |
 |
Por lo tanto: 
Þ 
Si se hace tender x a cero,
y al estar 
comprendido entre dos expresiones que tienden a 1 cuando x
® 0, también deberá tender a
1. Por lo tanto: 
.
Para que esta demostración pueda generalizarse falta analizar qué es lo que ocurre para valores negativos de x.
Se designa con (- x) a los valores negativos de x.
Como senx es una función impar, sen(-x) = -senx.
Por lo tanto:
Þ 
Nota.
El cociente 
es tanto más cercano a 1 cuanto más próximo a 0 se
considere el valor de x.
| Esto permite geométricamente interpretar que para medidas de arco muy pequeñas, sus correspondientes valores de sen x son aproximadamente iguales a x. |  |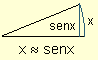
Ejemplo.
Halle el valor de 
Al evaluar numerador y denominador
en cero, resulta la indeterminación .
Para resolver este límite, se trata de escribir el cociente de
manera tal de poder aplicar el teorema anterior: 
Por propiedad de límite,
Además, si x ®
0, 2x también tiende a cero y por lo tanto:
En consecuencia, 
Ejemplo.
Calcule el valor de 
Sustituyendo la variable por 0 resulta una indeterminación.
Utilizando la identidad
es posible
transformar el cociente de manera tal de poder aplicar el teorema
anterior.
Por lo tanto: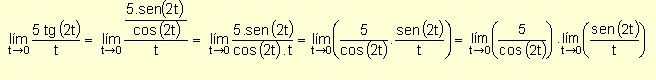 
Hallando el primer límite 
En el segundo límite
multiplicamos y dividimos por 2 y teniendo en cuenta que si t
® 0 también 2t ®
0 resulta que: 
Entonces: 
= 5.2 = 10
Ejemplo.
Halle
Reemplazando la variable por el valor al cual tiende
resulta la indeterminación .
Aplicando diferencia de cuadrados en el denominador y teniendo en cuenta que si x tiende a 3 entonces x - 3 tiende a 0 resulta:
| En este momento está en condiciones de realizar algunos ejercicios. |
[Volver a Límite de funciones] [Ir a Contenidos] [Ir a Inicio]
,
