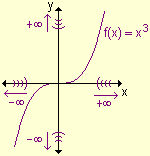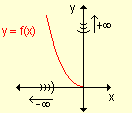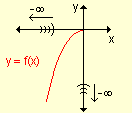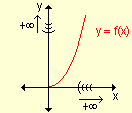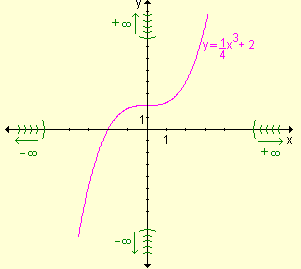[Volver a Límite de funciones] [Ir a Contenidos] [Ir a Inicio]

Límites infinitos en el infinito

En la siguiente tabla se presenta el análisis del comportamiento de funciones que crecen o decrecen indefinidamente cuando la variable también crece o decrece sin tope.

  
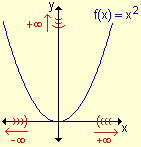
  • f(x) crece indefinidamente a medida que x crece indefinidamente.
  • f(x) crece indefinidamente a medida que x decrece indefinidamente

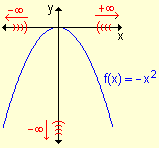
  • f(x) decrece indefinidamente a medida que x crece indefinidamente.
  • f(x) decrece indefinidamente a medida que x decrece indefinidamente

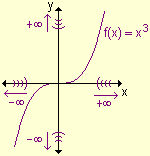
  • f(x) crece indefinidamente a medida que x crece indefinidamente.
  • f(x) decrece indefinidamente a medida que x decrece indefinidamente

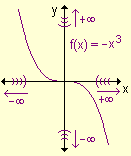
  • f(x) crece indefinidamente a medida que x decrece indefinidamente.
  • f(x) decrece indefinidamente a medida que x crece indefinidamente.

Estas funciones presentan comportamientos que no pueden describirse con la idea y el concepto de límite estudiado. Por lo tanto, debe extenderse dicho concepto para interpretar y simbolizar estas situaciones.

Simbólicamente se escribe:

  

Gráficamente

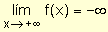{short description of image} para indicar que la función decrece indefinidamente cuando la variable crece indefinidamente.

  
 

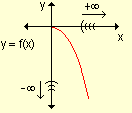
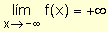{short description of image} para indicar que la función crece indefinidamente cuando la variable decrece indefinidamente.

  
 

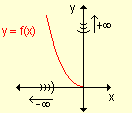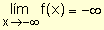{short description of image} para indicar que la función decrece indefinidamente cuando la variable decrece.

  
 

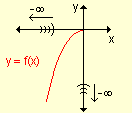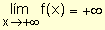{short description of image} para indicar que la función crece indefinidamente cuando la variable crece.

  

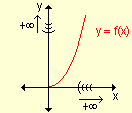Recordemos que en cualquiera de los límites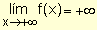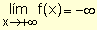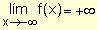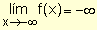{short description of image}, {short description of image}, {short description of image}, {short description of image}, es importante tener en cuenta que +¥ o -¥ no son números. En estos casos se dice que el límite no existe.

La expresión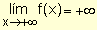{short description of image} significa que si x ® +¥ ; f(x) ® +¥ .

Es decir que para todo M > 0, existe k > 0 tal que si x > k, Þ f(x) > M. Esto significa que si x es positivo y grande, su correspondiente imagen f(x) también es positiva y grande.

    

Ejemplo. Discuta el comportamiento de la función y = 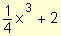{short description of image} para x ® +¥ y para x ® -¥ . Grafique.

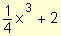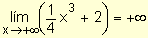
Cuando x ® +¥ , x3 ® +¥ y por lo tanto {short description of image} ® +¥ . Se puede escribir {short description of image}

Cuando x ® –¥ , x3 ® –¥ y por lo tanto 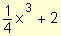{short description of image} ® –¥ .

Luego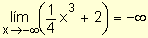{short description of image}

Su gráfica es

   

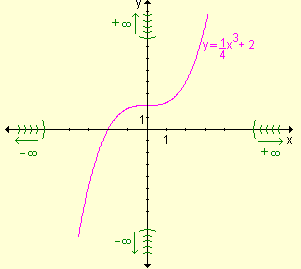
Le recomendamos que realice estos ejercicios, para su mejor comprensión.

[Volver a Límite de funciones] [Ir a Contenidos] [Ir a Inicio]