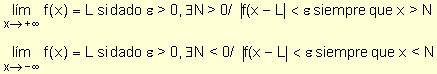[Volver
a Límite de funciones]
[Ir a Contenidos] [Ir a Inicio]
Límites
en el infinito
Analizaremos el comportamiento de
las funciones definidas gráficamente cuando x crece indefinidamente
y cuando x decrece indefinidamente
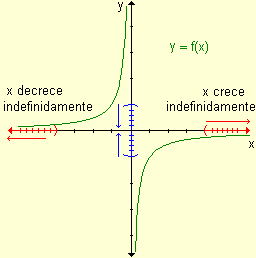
a) Si x crece
indefinidamente la función f(x) se acerca a 0.
b) Si x decrece
indefinidamente, los valores de la función se acercan a 0. |
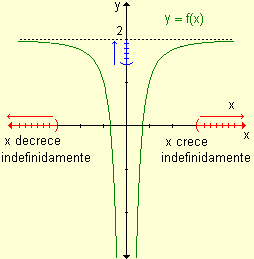
a) Si x crece
indefinidamente la función f(x) se acerca a 2.
b) Si x decrece
indefinidamente, los valores de la función se acercan a 2. |
|
La recta y
= 0 es asíntota horizontal
de la función. |
La recta y
= 2 es asíntota horizontal
de la función. |
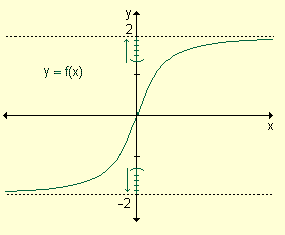
a) Si x crece
indefinidamente la función f(x) se acerca a 2.
b) Si x decrece
indefinidamente, los valores de la función se acercan a
-2. |
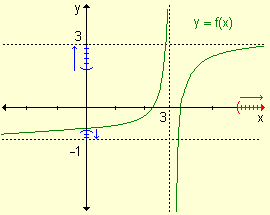
a) Si x crece
indefinidamente la función f(x) se aproxima a 3.
b) Si x decrece
indefinidamente, los valores de la función se aproximan a
-1. |
|
Las rectas y
= 2 e y
= -2
son asíntotas horizontales de la función. |
Las rectas y
= 3 e y
= -1
son asíntotas horizontales de la función. |
En el primer ejemplo anotamos
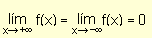 .
.
Recordemos que ¥
no representa un número. La expresión anterior expresa que
el límite de f(x) cuando x crece o decrece indefinidamente es cero.
El comportamiento de funciones que
se aproximan a un número cuando la variable crece o decrece
indefinidamente (x ® +¥
, x ® -¥)
se indica de la siguiente manera:
|
Simbólicamente se escribe |
Gráficamente: |
|
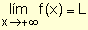 para indicar que la función tiende a L cuando los valores de x
crecen indefinida- mente.
para indicar que la función tiende a L cuando los valores de x
crecen indefinida- mente.
|
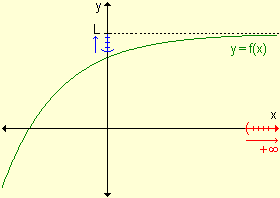 |
|
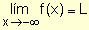 para indicar que la función tiende a L cuando los valores de x
decrecen indefinidamente.
para indicar que la función tiende a L cuando los valores de x
decrecen indefinidamente.
|
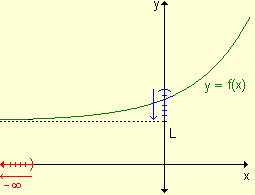 |
Formalizando la definición de límite
de una función que tiende a un número finito cuando la
variable independiente tiende a +¥
ó a -¥,
resulta:
Definición.
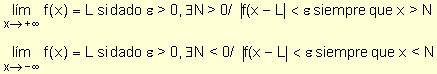
Las propiedades referidas al álgebra
de límites válidas si "x®
a" se cumplen también si "x®
+¥ " y "x®
–¥".
Ejemplo.
Calcule 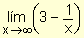 .
.
Cuando x toma valores grandes,
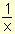 es pequeño. Tomando x suficientemente grande,
es pequeño. Tomando x suficientemente grande,
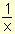 puede hacerse tan pequeño como queramos. Por lo tanto
puede hacerse tan pequeño como queramos. Por lo tanto
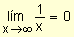 .
.
Por otra parte
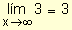
y como el límite de la
diferencia es la diferencia de los límites resulta:
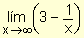 = 3 – 0 = 3
= 3 – 0 = 3
Problema.
Se proyecta que dentro de t años,
la población de cierto pueblo será p(t) =
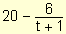 miles de personas. ¿Qué se espera que suceda con la población
a medida que el tiempo transcurre indefinidamente?
miles de personas. ¿Qué se espera que suceda con la población
a medida que el tiempo transcurre indefinidamente?
Solución.
Para determinar el
comportamiento de la función cuando el tiempo transcurre
indefinidamente se debe calcular el límite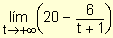 .
.
Cuando t ®
+¥ , también t +1®
+¥ y, por lo tanto,
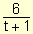 ®
0.
®
0.
En consecuencia
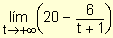 = 20. Esto expresa que a medida que el tiempo
transcurre, la población tiende a estabilizarse en 20 000 personas.
= 20. Esto expresa que a medida que el tiempo
transcurre, la población tiende a estabilizarse en 20 000 personas.
[Volver
a Límite de funciones]
[Ir a Contenidos] [Ir a Inicio]