[Volver a Límite de funciones] [Ir a Contenidos] [Ir a Inicio]

Límite de una función polinomial

El límite de una función polinomial en el infinito, es igual al límite del término de mayor grado. Dada una función polinomial de grado n > 0,

p(x) = a₀ xⁿ + a₁ x^n-1 + a₂ x^n-2 + ...+ a_n

se cumple

Para demostrar esta afirmación escribimos:

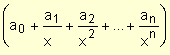p(x) = a₀ xⁿ + a₁ x^n-1 + a₂ x^n-2 + ...+ a_n = . xⁿ

Entonces el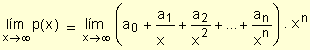

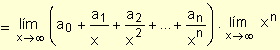
Como 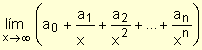= a0 podemos asegurar que:

Ejemplo. Halle .

Por lo analizado anteriormente

Nota. En el cuadro siguiente se muestran las distintas posibilidades con respecto al límite en el infinito de una función polinomial.

El coeficiente principal es positivo.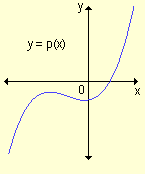      p(x)® -¥ cuando x ® -¥      p(x)® +¥ cuando x ® +¥	El coeficiente principal es negativo. 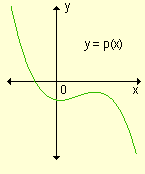   p(x)® +¥ cuando x ® -¥      p(x)® -¥ cuando x ® +¥
El coeficiente principal es positivo.      p(x)® +¥ cuando x ® -¥       p(x)® +¥ cuando x ® +¥	El coeficiente principal es negativo.    p(x)® ¥ cuando x ® -¥      p(x)® -¥ cuando x ® +¥

Nota. Determinar si una función tiene o no límite en el infinito es útil para analizar el comportamiento asintótico de su gráfica.

[Volver a Límite de funciones] [Ir a Contenidos] [Ir a Inicio]