[Volver a Los números reales y la recta real] [Ir a Contenidos] [Ir a Inicio]

Valor absoluto

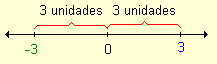
En la siguiente gráfica, los números -3 y 3 representan las coordenadas de dos puntos distintos en la recta numérica. Sin embargo, ambos están situados a la misma distancia del 0.

	El punto correspondiente a - 3 está situado a la izquierda del 0 a la misma distancia que el punto correspondiente a 3 que se encuentra situado a la derecha.
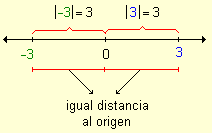
	Esto se indica con la notación valor absoluto: ½ - 3½ = 3: valor absoluto de -3 es 3. ½ 3½ = 3: valor absoluto de 3 es 3.
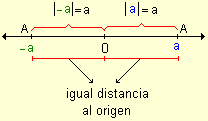
Si a es un número real entonces a es la coordenada o abscisa del punto A sobre la recta real o numérica. El símbolo ½ a½ indica el número de unidades entre el punto A y el origen. El número ½ a½ , no negativo, se llama valor absoluto de a.

Para un número positivo a resulta que su valor absoluto coincide con él mientras que si el número es negativo su valor absoluto es el opuesto de a. Además como 0 es el origen es evidente que ½ 0½ = 0.

Desde el punto de vista geométrico el valor absoluto de un número es la distancia entre el punto y el origen.

Desde el punto de vista algebraico, se define el valor absoluto de un número de la siguiente manera:

½ a½ =

El valor absoluto de todo número real es un número no negativo.

En símbolos:

Propiedades del valor absoluto

• ½ a.b½ = ½ a½ .½ b½ , " a, " b

• , " a, " b ¹ 0

• ½ a + b½ £ ½ a½ +½ b½ , donde a, b Î R (desigualdad triangular)

• " a : ½ a½ = ½ -a½

Distancia entre dos puntos

El concepto de valor absoluto permite definir la distancia entre dos puntos cualesquiera de la recta real. Por ejemplo, la distancia entre los puntos de abscisas 3 y 8, es 5.

Esta distancia se obtiene al restar las coordenadas de los puntos: 8 - 3 = 5.

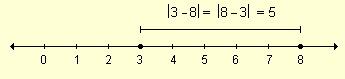
Utilizando valor absoluto ½ 8 - 3½ = 5. Como ½ 3 - 8½ también es 5, se concluye que no importa el orden en el que se realice la resta.

De la misma manera si se desea determinar la distancia entre los puntos de abscisas -2 y 5:

½ 5 - (-2)½ = ½ 5 + 2½ = ½ 7½ = 7 ½ - 2 - 5 ½  = ½ -7½ = 7

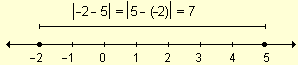Para calcular la distancia entre dos puntos ubicados a la izquierda del origen, se obtiene:

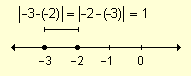½ - 3- (-2)½ = ½ - 3 + 2½ = ½ - 1½ = 1 ½ - 2- (-3)½ = ½ - 2 + 3½ = ½ 1½ = 1

Definición. Sean a y b las coordenadas o abscisas de los puntos A y B sobre la recta real. La distancia entre ellos está dada por:

d(A, B) = ½ a - b½ = ½ b - a½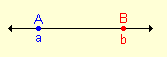

Se puede observar que la distancia entre el origen O y el punto A está dada por:

d(A, 0) = ½ a - 0½ = ½ 0 - a½ = ½ a½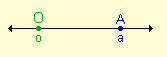

El concepto de valor absoluto de un número se emplea en algunas definiciones importantes en el estudio del Cálculo. Se resolverán ecuaciones e inecuaciones en las que interviene dicho concepto.

Ejemplos. Determine él o los valores de x que verifican cada igualdad o desigualdad:

· ½ x½ = 3

Desde el punto de vista geométrico ½ x½ = 3 significa que la distancia del o los valores de x al cero debe ser tres. De aquí resulta que las soluciones de esta ecuación son x = 3 y x = -3.

S = { 3 ; –3}

· ½ x½ < 3

En este ejemplo se deben considerar todos los números que distan del origen menos de tres unidades. La solución de la inecuación son todos los números reales entre - 3 y 3, es decir, - 3 < x < 3. Resulta el intervalo abierto (-3, 3).

S = { x / -3 < x < 3} = (-3, 3)

· ½ x½ £ 3

Los valores de x que satisfacen la desigualdad son todos los que se encuentran a una distancia del cero menor o igual a tres. Por lo tanto el conjunto solución está formado por –3, 3 y todos los números reales comprendidos entre ellos. Resulta el intervalo cerrado [-3, 3].

S = { x / -3 £ x £ 3} = [-3, 3]

· ½ x½ > 3

Realizando el mismo análisis que en los ejemplos anteriores, resulta que los valores de x que verifican la desigualdad son aquellos que están a más de 3 unidades del origen. La solución es el conjunto de los números reales mayores que 3 o menores que -3. La solución se puede escribir como unión de dos intervalos abiertos: (-¥ , -3) È (3, +¥ ).

S = { x / x £ -3 ó x ³ 3} = (-¥ , -3) È (3, +¥ )

· ½ x½ ³ 3

La solución es el conjunto de números reales mayores o iguales que 3 o menores o iguales que - 3. Por lo tanto,½ x½ ³ 3 Û x £ -3 ó x ³ 3.  Utilizando la notación de intervalos podemos escribir (-¥ , - 3] È [3, +¥ ).

S = { x / x £ -3 ó x ³ 3} = (-¥ , - 3] È [3, +¥ )

Resumiendo todas las situaciones en un mismo gráfico resulta:

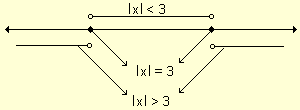
De estos ejemplos se deducen las siguientes propiedades:

Propiedad 1. Sea k Î R tal que k > 0, ½ a½ = k Û a = k ó a = -k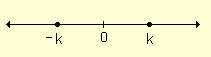
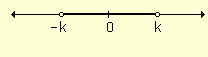
Propiedad 2. ½ a½ < k Û -k < a < k Esta propiedad también es válida al considerar la desigualdad "£ " ½ a½ £ k Û -k £ a £ k
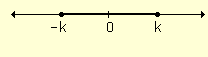Propiedad 3. ½ a½ > k Û a < -k ó a > k    También vale para "³ " ½ a½ ³ k Û a £ -k ó a ³ k.

Ejemplos. Resuelva las siguientes igualdades y desigualdades.

· ½ x - 2½ = 8

Por propiedad 1 puede ocurrir que x - 2 = 8 ó x - 2 = - 8 y resulta que x = 10 ó x = - 6

Desde el punto de vista geométrico los puntos de abscisas 10 y -6 están ubicados a 8 unidades de 2.

· ½ x - 3½ £ 7

Teniendo en cuenta la propiedad 2:

-7 £ x - 3 £ 7 Þ -7 + 3 £ x £ 7+3 Þ -4 £ x £ 10

La solución es el intervalo cerrado [-4, 10]. Geométricamente representa el conjunto de puntos de la recta cuya distancia a 3 es menor o igual que 7.

· ½ x + 4½ > 5

Según la propiedad 3 resulta: x + 4 > 5 ó x + 4 < -5

x > 1 ó x < -9

Geométricamente representa el conjunto de puntos de la recta cuya distancia a - 4  es mayor que 5.   La solución está representada por la unión de los intervalos abiertos: (-¥ , -9) È (1,+¥ ).

· 0 <½ x - 5½ < 3

Debemos encontrar los valores de x que verifican ½ x - 5½ < 3 y 0 < ½ x - 5½

La primera desigualdad implica:

-3 < x - 5 < 3 Þ -3 + 5 < x < 3 + 5 Þ 2 < x < 8

Además se debe verificar que 0 < ½ x - 5½ . Como el valor absoluto es siempre positivo o nulo, los únicos valores de x que no verifican la desigualdad anterior son los que anulan ½ x - 5½.

Resolver ½ x - 5½ > 0 es equivalente a resolver ½ x - 5½ ¹ 0, de donde,  x ¹ 5.

La solución es la unión de dos intervalos (2, 5) È (5, 8). Geométricamente representa el conjunto de puntos de la recta cuya distancia al 5 es menor que 3 pero distinta a 0.

Ejemplo. Sea el conjunto C = {x / x Î R Ù ½ 3x - (x - 6)½ £ 5}. Grafíquelo e indique el intervalo que determina.

Aplicando la propiedad ½ a½ < k Û -k < a < k y resolviendo se obtiene:

-5 £ 3x - (x - 6) £ 5   Þ   -5 £ 3x - x + 6 £ 5   Þ   -5 £ 2x + 6 £ 5   Þ   

-5 - 6 £ 2x £ 5 - 6   Þ   - 11 £ 2x £ - 1   Þ  

La solución es el conjunto de todos los números reales comprendidos entre y , incluidos los extremos que representa el intervalo cerrado .

Su gráfica es:               

Ejemplo. Sea el conjunto F = {x / x Î R Ù ½ 3x - (m - x)½ < 3}. Determine el valor de m para que resulte el conjunto de todos los números reales que están a menos de unidades de distancia de - .

Representando gráficamente todos los valores de x que están a menos de unidades de distancia de - resulta el intervalo , o sea .

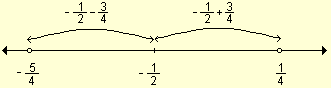
Para encontrar el valor de m, se resuelve la desigualdad: ½ 3x - m + x½ < 3 Þ ½ 4x - m½ < 3

Sacando factor común 4 y aplicando las propiedades del valor absoluto: 4 Þ

Por lo tanto Þ m = -2.

O también: ½ 3x - m + x½ < 3 Þ ½ 4x - m½ < 3 Þ - 3 < 4x - m < 3 Þ

Por lo tanto debe verificarse = y = .

Resolviendo la primera se obtiene:

= Þ -3 + m = -5 Þ m = -5 + 3 Þ m = -2

Este valor de  m  verifica la otra igualdad,  por lo tanto para que el conjunto  F  represente el  conjunto pedido,  m = -2.

Ejemplo. Sea el conjunto D = {x / x Î R Ù 0 <½ (x - 1).2 - x½ < 4}. Grafíquelo e indique el o los intervalos que determina.

Si 0 <½ (x - 1).2 - x½ < 4 Þ 0 <½ 2x – 2 – x½ < 4 Þ 0 <½ x – 2½ < 4.

Para resolver esta desigualdad se debe tener en cuenta que ½ x - 2½ < 4 y a la vez ½ x - 2½ > 0. De acuerdo a la propiedad 2 de valor absoluto resulta:

½ x - 2½ < 4 Þ - 4 < x - 2 < 4 Þ - 4 + 2 < x < 4 + 2 Þ - 2 < x < 6

La desigualdad ½ x - 2½ > 0 se verifica para todo valor real de x excepto para el que la diferencia x - 2 es nula.

La inecuación ½ x - 2½ > 0 es equivalente a x - 2 ¹ 0.

La solución es el conjunto de los números reales excepto el valor 2 (x ¹ 2).

Teniendo en cuenta las soluciones obtenidas de ambas desigualdades, se puede decir que el conjunto solución está formado por todos los números reales comprendidos entre –2 y 6 excepto 2 que se puede expresar como la unión de dos intervalos, (-2, 2) È (2, 6).

Ejemplo. Encuentre el valor de m de manera tal que la desigualdad 0 < ½ x + 2m½ < - 8m tenga como solución a (–3,1) È (1,5).

Los números reales pertenecientes a (–3,1) È (1,5) son los que verifican -3 < x < 5 y x ¹ 1.

La expresión  ½ x + 2m½ < -8m  se verifica para todos los valores de  x  que están a una distancia menor que   -8m de -2m. Por lo tanto -2m = 1 y -8m = 4, de donde resulta m = .

También se puede encontrar el valor de m resolviendo la desigualdad dada.

A partir de½ x + 2m½ < -8m se obtiene:

8m < x + 2m < -8m Þ 8m - 2m < x < -8m - 2m Þ 6m < x < - 10m

Además, de la expresión ½ x + 2m½ > 0, se deduce: x + 2m ¹ 0 Þ x ¹ -2m

Comparando las desigualdades, se debe cumplir que: 6m = -3 y -10m = 5, de donde m = .

Se verifica además que para m = el valor de x resulta distinto de 1.

[Volver a Los números reales y la recta real] [Ir a Contenidos] [Ir a Inicio]