[Volver a Función continua] [Ir a Contenidos] [Ir a Inicio]
Teoremas de las funciones continuas
Las funciones que son continuas en un intervalo cerrado tienen ciertas propiedades especiales que se enuncian a continuación:
Teorema de la conservación del signo
Si f(x) es continua en x = a y f(a) > 0, existe un intervalo abierto tal que f(x) > 0, " x Î (a - d , a + d ).
Actividad de reflexión
A) i) Realice los pasos que se detallan a continuación para definir gráficamente una función y = f(x).
a) Grafique un sistema de ejes coordenados cartesianos.
b) Sobre el eje x elija dos valores a y b, con a < b.
c) Sobre el eje y determine los valores f(a) y f(b).
d)
Marque los puntos ![]() y
y ![]() .
.
e) Sobre el eje y determine un valor k que se encuentre entre f(a) y f(b).
f) Grafique la recta y = k, paralela al eje x.
g)
Grafique una función continua y = f(x)
uniendo los puntos ![]() y
y ![]() .
.
h) La gráfica de la función y = f(x) , ¿interseca a la recta y = k? ¿En cuántos puntos?
ii) Repita la actividad (i) graficando otras funciones.
Según lo observado extraiga conclusiones.
B) Para el mismo caso que la
situación (A), grafique una función desde
![]() hasta
hasta
![]() pero
que no interseque a la recta y = k.
pero
que no interseque a la recta y = k.
¿Qué análisis puede hacer sobre la función?
De la actividad anterior se enuncia el siguiente teorema:
Teorema del valor intermedio
Si y = f(x) es una función continua en el intervalo cerrado [a, b] donde f(a) ¹ f(b) y k es un número real cualquiera comprendido entre f(a) y f(b), existe al menos un número real c perteneciente al intervalo (a, b) tal que f(c) = k.
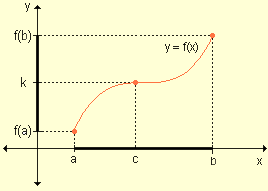
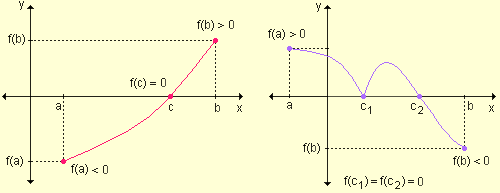
Desde el punto de vista geométrico, este teorema establece que la gráfica de una función continua en un intervalo cerrado, debe intersecar al menos una vez a cada recta de ecuación y = k, siendo f(a) < k < f(b).
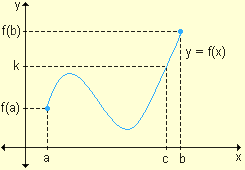
En el siguiente ejemplo se presenta la importancia de la verificación de la condición de continuidad de la función y = f(x) en el intervalo [a, b] para poder garantizar la existencia del número real c.
Ejemplo. Sea la función
f(x) = 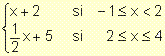 .
¿Es posible aplicar el teorema del valor intermedio en su dominio de definición?
Justifique.
.
¿Es posible aplicar el teorema del valor intermedio en su dominio de definición?
Justifique.
El dominio es el intervalo cerrado [-1, 4]. Además, f(-1) = 1 y f(4) = 7.
Cada tramo es una función polinomial y por lo tanto cada tramo es continuo en el intervalo dado. Debe analizarse la continuidad de la función en x = 2:
![]() y
y ![]() .
.
Como los límites laterales son distintos, la función no es continua en x = 2 y por lo tanto tampoco es continua en el intervalo cerrado [-1, 4]. Por este motivo, no puede aplicarse el teorema del valor intermedio.
| La gráfica de la
función dada es la siguiente: |
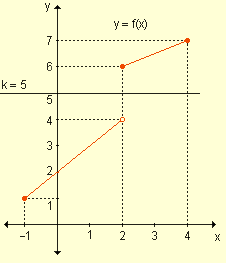 |
|
Si k es cualquier número real cualquiera comprendido entre 4 (inclusive) y 6, por ejemplo k = 5, no existe ningún valor de c perteneciente al intervalo (-1, 4), tal que f(c) = 5. |
||
El teorema del valor intermedio también resulta útil para determinar la existencia de raíces de una función continua en un intervalo cerrado.
Sea y = f(x) una función continua en el intervalo cerrado [a, b] tal que f(a) y f(b) toman valores de signos contrarios. Es posible asignarle a k el valor cero, ya que cero está comprendido entre f(a) y f(b), de manera tal que en el intervalo (a, b) existe por lo menos un número real c tal que f(c) = 0. De esta manera puede concluirse que c es una raíz real de la función dada.
Esto se enuncia en el siguiente teorema:
Teorema de Bolzano
Si y = f(x) es una función continua en el intervalo cerrado [a, b] y f(a) y f(b) tienen signos opuestos, entonces existe al menos un número real c perteneciente al intervalo (a, b) tal que f(c) = 0; es decir, c es una raíz de f(x).
Las siguientes gráficas permiten ilustrar el teorema:
Ejemplo.
Sea la función g(x) =
![]() .
Determine si tiene una raíz real en el intervalo [-5,
1]. Justifique la respuesta.
.
Determine si tiene una raíz real en el intervalo [-5,
1]. Justifique la respuesta.
El dominio de esta función es D = R - {-3} y por lo tanto no es continua en el intervalo [-5, 1]. Como no se cumple la hipótesis de continuidad del teorema de Bolzano, no puede garantizarse la existencia de una raíz real en el intervalo dado.
Ejemplo. Dada la
función definida por la ley h(x) =
![]() .
Determine si tiene al menos una raíz real en el intervalo [0, 2].
Justifique la respuesta.
.
Determine si tiene al menos una raíz real en el intervalo [0, 2].
Justifique la respuesta.
El dominio de la función es D = R - {-1} y, por lo tanto, es continua en el intervalo [0, 2]. Luego se calculan los valores de la función en los extremos del intervalo:
h(0) =
![]() y h(2)
=
y h(2)
= ![]()
Como en los extremos del intervalo la función toma valores de signo contrario, cumple con las hipótesis del teorema de Bolzano y por lo tanto se puede asegurar que existe al menos una raíz real en dicho intervalo, es decir, que existe al menos un valor real de c tal que h(c) = 0.
h(c) = 0
Þ ![]() Þ 2(2c - 3)
= 0 Þ 4c
- 6 = 0
Þ c =
Þ 2(2c - 3)
= 0 Þ 4c
- 6 = 0
Þ c =
![]() .
.
La raíz buscada que pertenece
al intervalo [0, 2] es x =
![]() .
.
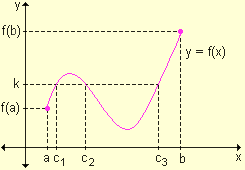
Ejemplo. Sea g(x) una función continua en el intervalo [-3, 6] tal que g(-3) = 2, g(1) = 1, g(2) = -3 y g(6) = g(4) siendo ambos positivos. Interprete gráficamente e indique el menor número de raíces que g(x) puede tener en dicho intervalo.
Graficando las condiciones solicitadas se obtiene:
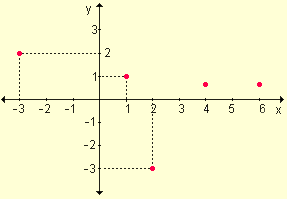 Una gráfica posible de la función es: |
Teniendo en cuenta que las imágenes de 6 y de 4 son positivas, la gráfica de una función continua en el intervalo [-3, 6] cortará al eje de las abscisas por lo menos en dos puntos, uno perteneciente al intervalo (2, 4) y el otro al (1, 2). Por lo tanto, la función tendrá como mínimo, dos raíces en dicho intervalo. 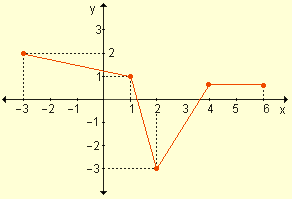 |
| En este momento le sugerimos que realice estos ejercicios para corroborar sus conocimientos |
[Volver a Función continua] [Ir a Contenidos] [Ir a Inicio]