También se clasifica como evitable la discontinuidad en la que no se cumple la condición (c) de la definición de continuidad, es decir, existen f(a) y
[Volver a Función continua] [Ir a Contenidos] [Ir a Inicio]
Tipos de discontinuidades
Las discontinuidades se clasifican en:
Discontinuidad evitable
En
este caso no se cumple la condición (a) de la definición de
continuidad, es decir existe el límite finito L de f(x) en x
= a pero
f(x) no está definida en a. La función puede modificarse
adoptando como f(a) el valor L correspondiente, convirtiéndose así
en una función continua en x =
a.
También
se clasifica como evitable la discontinuidad en la que no se cumple la
condición (c) de la definición de continuidad, es decir,
existen f(a) y ![]() ,
pero no coinciden. En este caso, puede salvarse la discontinuidad tomando
como valor de la función el resultado del límite.
,
pero no coinciden. En este caso, puede salvarse la discontinuidad tomando
como valor de la función el resultado del límite.
Discontinuidad de salto
Existen los límites laterales pero son distintos.
Discontinuidad infinita
Al menos uno de los límites laterales no existe.
Ejemplo. Dadas las siguientes gráficas de funciones discontinuas en x = 5, indique el tipo de discontinuidad en cada caso.
i) 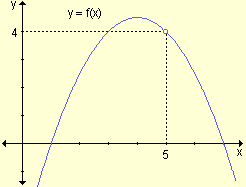 |
ii)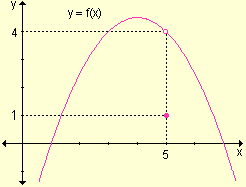 |
iii)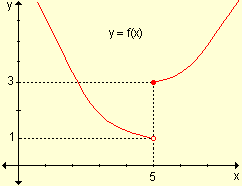 |
iv)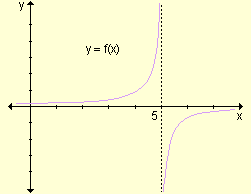 |
i) El límite de y = f(x) para x tendiendo a 5 existe y es 4, pero 5 no pertenece al dominio de la función. Se trata de un discontinuidad evitable en x = 5.
ii) Al igual que en (i) el límite para x ® 5 existe y es 4 pero no coincide con la imagen de 5, que es 1. Se trata de una discontinuidad evitable.
iii) Observando la gráfica
se deduce que ![]() y
y ![]() . Como
los límites laterales existen pero son distintos es una
discontinuidad de salto.
. Como
los límites laterales existen pero son distintos es una
discontinuidad de salto.
iv) Los límites
laterales no existen pues ![]() y
y ![]() . La
función presenta una discontinuidad infinita en x
= 5.
. La
función presenta una discontinuidad infinita en x
= 5.
Ejemplo. Dada la
función g : R ® R / x
® 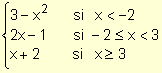 indique sus puntos de discontinuidad, si existen, y clasifíquelos.
indique sus puntos de discontinuidad, si existen, y clasifíquelos.
Los posibles puntos de discontinuidad son x = -2 y x = 3, ya que en los demás puntos g(x) es continua, debido a que las leyes que definen cada tramo son expresiones polinómicas.
En x =
-2: ![]() =
3 - (-2)2
=
-1 y
=
3 - (-2)2
=
-1 y ![]() = 2.(-2)
- 1 =
-5. Los límites laterales existen pero
son distintos, por lo tanto, no existe el límite cuando x tiende a
-2. La función presenta una
discontinuidad de salto en x =
-2.
= 2.(-2)
- 1 =
-5. Los límites laterales existen pero
son distintos, por lo tanto, no existe el límite cuando x tiende a
-2. La función presenta una
discontinuidad de salto en x =
-2.
En x =
3: ![]() =
2.3 - 1 =
5 y
=
2.3 - 1 =
5 y ![]() = 3 + 2
=
5. Los límites laterales existen y son iguales, por lo tanto, el límite
cuando x tiende a 3 es 5. La imagen de 3 también es 5, en
consecuencia, la función es continua en x =
3.
= 3 + 2
=
5. Los límites laterales existen y son iguales, por lo tanto, el límite
cuando x tiende a 3 es 5. La imagen de 3 también es 5, en
consecuencia, la función es continua en x =
3.
Este análisis puede visualizarse gráficamente:
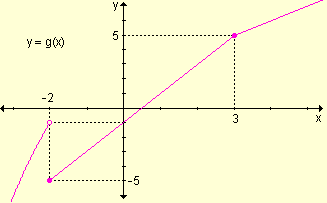
Ejemplo. Grafique la
función m : R ® R / m(x)
=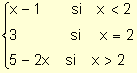 y analice su continuidad en x = 2.
y analice su continuidad en x = 2.
Su gráfica es:
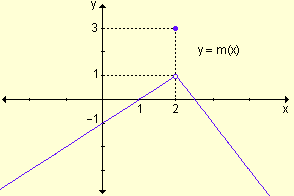
Se observa que la función es discontinua en x = 2.
m(2) = 3.
Calculando los límites laterales: ![]() y
y ![]()
Como los límites laterales
existen y son iguales, entonces ![]()
Luego ![]() ¹ m(2)
¹ m(2)
Por lo tanto, la función presenta una discontinuidad evitable en x = 2.
Se puede volver a definir la función para que resulte continua en x = 2. Para ello se le asigna como imagen de 2 el resultado del límite, es decir:
m: R ®
R / m*(x) =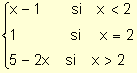
La gráfica de la función redefinida resulta:
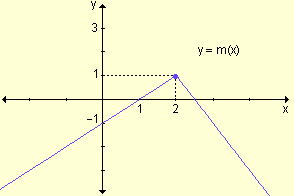
Ejemplo. Analice la
continuidad de la función f(x) =
![]() .
.
Por ser un cociente de funciones polinomiales la función es continua para todo valor real de x, excepto en x = 2 ya que este valor anula el denominador.
Como existe el límite pero la función no está definida en x = 2, presenta una discontinuidad evitable en dicho punto.
Es posible redefinirla para que resulte continua. Para ello se le asigna a x = 2, el valor del límite.
Resulta: f(x) =
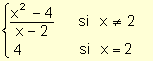 .
.
| En este momento le sugerimos que realice estos ejercicios para corroborar sus conocimientos |
[Volver a Función continua] [Ir a Contenidos] [Ir a Inicio]