[Volver
a Límite de funciones]
[Ir a Contenidos] [Ir a Inicio]
Límites
infinitos
Analicemos, a partir de su gráfica,
la existencia de los límites.
|
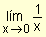
|
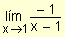
|
|
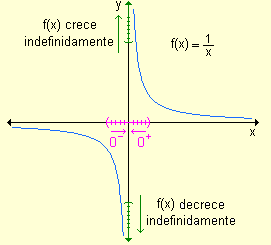
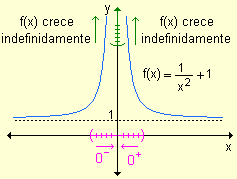
Las dos ramas de la curva se
acercan cada vez más al eje y a medida que x se aproxima a
cero.
Para esta gráfica la
recta x = 0
es asíntota vertical. |
Las dos ramas de la curva se
acercan cada vez más a la recta x =
1 a medida que x se aproxima a ese valor.
Para esta gráfica la
recta x = 1
es asíntota vertical. |
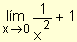
|
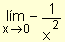
|
|
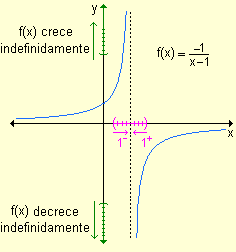
Para esta gráfica la
recta x = 0
es asíntota vertical. |
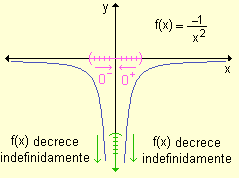
Para esta gráfica la
recta x = 0
es asíntota vertical. |
El comportamiento de estas
funciones no puede describirse con la idea y el concepto de límite
que se ha estudiado hasta ahora.
Analizando nuevamente la función
y = 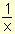 ,
se observa en la gráfica que cuando x ®
0+, los valores de f crecen más allá de todo
tope. Por lo tanto f no tiene límite cuando x ®
0+. Sin embargo resulta conveniente decir que f(x) se aproxima
a ¥ cuando x
® 0+. Se escribe
,
se observa en la gráfica que cuando x ®
0+, los valores de f crecen más allá de todo
tope. Por lo tanto f no tiene límite cuando x ®
0+. Sin embargo resulta conveniente decir que f(x) se aproxima
a ¥ cuando x
® 0+. Se escribe
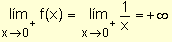 .
.
Esto no significa que el límite
existe ni que +¥ es un número
real, sino que expresa que la función se hace tan grande como
deseamos escogiendo x suficientemente cercano a cero.
Resumen
| Simbólicamente se escribe: |
Gráficamente: |
|
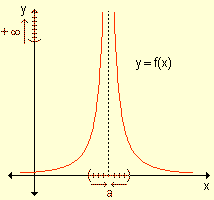
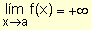 para indicar que los valores de la función crecen
indefinidamente (sin tope) cuando x se acerca a "a" por
izquierda y por derecha.
para indicar que los valores de la función crecen
indefinidamente (sin tope) cuando x se acerca a "a" por
izquierda y por derecha.
|
 |
|
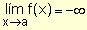 para indicar que los valores de la función decrecen
indefinidamente (sin tope) cuando x se aproxima a "a" por
valores menores y mayores que él.
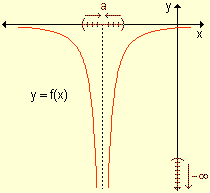
para indicar que los valores de la función decrecen
indefinidamente (sin tope) cuando x se aproxima a "a" por
valores menores y mayores que él.
|
|
|
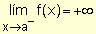 para indicar que los valores de la función crecen
indefinidamente cuando x se aproxima a "a" por valores
menores que él.
para indicar que los valores de la función crecen
indefinidamente cuando x se aproxima a "a" por valores
menores que él.
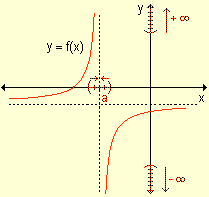
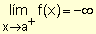 para
indicar que los valores de la función decrecen indefinidamente
cuando x se aproxima a "a" por valores mayores que él. para
indicar que los valores de la función decrecen indefinidamente
cuando x se aproxima a "a" por valores mayores que él. |
|
|
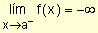 para indicar que los valores de la función decrecen
indefinidamente cuando x se acerca a "a" por valores menores
que él.
para indicar que los valores de la función decrecen
indefinidamente cuando x se acerca a "a" por valores menores
que él.
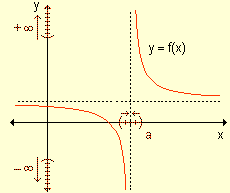
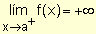 para indicar que los valores de la función crecen
indefinidamente cuando x se acerca a "a" por valores mayores
que él.
para indicar que los valores de la función crecen
indefinidamente cuando x se acerca a "a" por valores mayores
que él.
|
 |
Nota.
Cuando se refiere a límites infinitos en
realidad no son límites sino que proporcionan símbolos y un
lenguaje útiles para describir el comportamiento de funciones cuyos
valores se hacen arbitrariamente grandes (positivos o negativos).
Ejemplo.
Sea la gráfica de la función f(x) =
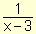 :
:
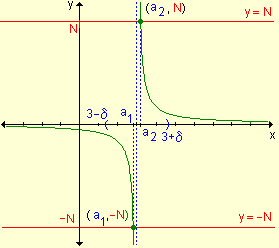
Observando la gráfica se
puede escribir: 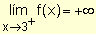 y
y 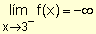
Trazando rectas horizontales de
ordenada N y -N, tan grandes como se quiera en
valor absoluto, quedan determinados dos puntos sobre la gráfica (a1,
-N) y (a2, N) tal que para x
Î (a1, a2) los
respectivos valores absolutos de f(x) superan a N. De esta manera, al
aproximarse x a 3 por izquierda o por derecha, se obtienen ordenadas que
superan cualquier valor real preestablecido.
Del análisis de este ejemplo
se formaliza la definición de la noción de límite de
una función que tiende a +¥
ó a -¥
cuando la variable tiende a un número finito.
Definición.
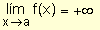 si dado un número N >
0, $ d >
0 / f(x) >
N siempre que 0 <
½ x -
a½
<
d .
si dado un número N >
0, $ d >
0 / f(x) >
N siempre que 0 <
½ x -
a½
<
d .
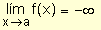 si dado un número N <
0, $ d >
0 / f(x) <
N siempre que 0 <
½ x -
a½
<
d .
si dado un número N <
0, $ d >
0 / f(x) <
N siempre que 0 <
½ x -
a½
<
d .
Ejemplos.
Determine los siguientes límites
a)
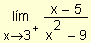 b)
b)
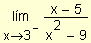 c)
c)
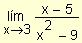
a)
= 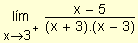
Cuando x ® 3 el
denominador tiende a cero y la expresión tiende a
¥ .
Cuando x se aproxima a 3 por derecha, la expresión
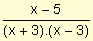 es negativa pues el numerador es negativo y cada uno de los factores del
denominador es positivo. Por lo tanto, el límite es
-¥
.
es negativa pues el numerador es negativo y cada uno de los factores del
denominador es positivo. Por lo tanto, el límite es
-¥
.
b)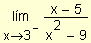 =
=
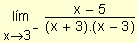
Cuando x ® 3 el
denominador tiende a cero y la expresión tiende a
¥ .
Cuando x se aproxima a 3 por izquierda, la expresión
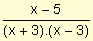 es positiva, pues el numerador es negativo, el factor (x + 3) es positivo
y (x - 3) negativo. Por lo tanto, el límite
es +¥ .
es positiva, pues el numerador es negativo, el factor (x + 3) es positivo
y (x - 3) negativo. Por lo tanto, el límite
es +¥ .
c)
El límite para x ® 3 no existe.
[Volver
a Límite de funciones]
[Ir a Contenidos] [Ir a Inicio]
![]()

![]()







