[Volver a Límite de funciones] [Ir a Contenidos] [Ir a Inicio]

Definición de límite

Para  llegar a una  definición  formal del concepto de  límite  se  retoma el  ejemplo  en el cual  dada la  función f(x) = con dominio D = {x / x Î R Ù x ¹ 1}, se obtuvo que = 6.

Para profundizar el significado de la expresión: f(x) tiende a 6 cuando x tiende a 1, se estudiará el comportamiento de las distancias entre x y 1 y entre f(x) y 6. Se agregan a las tablas confeccionadas anteriormente dos columnas encabezadas por  y  .

Observando las tablas surge que cuando x difiere de 1 en ±0,1, la función f(x) difiere de 6 en ±0,3 y cuando x difiere de 1 en ±0,001 la función difiere de 6 en ±0,003.

Esto puede expresarse de otro modo diciendo que los valores de f pueden hacerse tan próximos a 6 como se quiera, tomando x suficientemente próximo a 1.

Más precisamente, puede hacerse el valor absoluto de la diferencia tan pequeño como se quiera, tomando suficientemente pequeño el valor absoluto de la diferencia, .

Por ejemplo, si se desea que < 0,45 se debe tener en cuenta:

=

=

= 3 < 0,15

De esta manera, para que < 0,45 bastará con tomar siendo x ¹ 1.

Así se ha probado que si , o bien,  expresado de otra manera:

Resulta útil visualizar gráficamente esta situación.

Para ello, se debe tener en cuenta que, si x ¹ 1,  x - 1 ¹ 0  Þ  f(x) =

De esta manera, la gráfica de la función f(x) = es la recta y = 3x + 3 excluido el punto (1, 4) pues la función no está definida para x = 1.

Si x ¹ 1 Ù 1 – 0,15 < x < 1 + 0,15, entonces 6 – 0,45 < f(x) < 6 + 0,45.

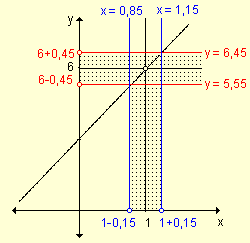
La parte de gráfica encerrada entre las rectas verticales x = 0,85 y x = 1,15 también queda encerrada entre las rectas horizontales y = 5,55 e y = 6,45.

El procedimiento realizado podría repetirse fijando otros valores para ½ f(x) - 6½ . A esos valores (positivos) se los llama, en forma genérica, e (épsilon) y para cada uno de ellos se obtiene un valor d (delta) también positivo, tal que: si x ¹ 1 y 1- d < x < 1+d , entonces 6 - e < f(x) < 6+ e .

Utilizando notación de distancia. Si x ¹ 1 y ½ x- 1½ < d entonces ½ f(x) - 6½ < e

o en forma equivalente: si x ¹ 1 Ù x Î (1 - d , 1 + d ) Þ f(x) Î (6 - e , 6 + e )

Gráficamente significa que la parte de gráfica encerrada entre las rectas verticales  x = 1 - d   y   x = 1 + d, también queda encerrada entre las rectas horizontales  y = 6 - e   e   y = 6 + e .

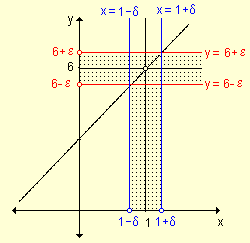
Puede decirse que = 6.

Definición de límite

(por pequeño que sea), $ d > 0 / ½ f(x) - L ½ < e para 0 < ½ x - a ½ < d .

o bien:

½ x - a½ < d Þ ½ f(x) - L ½ < e

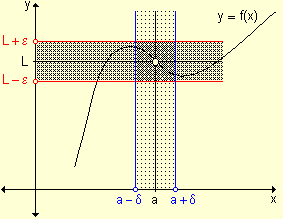
Esta definición establece que los valores de la función y = f(x) se aproximan al límite L conforme x lo hace al número a si el valor absoluto de la diferencia entre f(x) y L puede hacerse tan pequeña como se desee tomando x suficientemente cerca de a pero no igual a a.

Gráficamente:

[Volver a Límite de funciones] [Ir a Contenidos] [Ir a Inicio]